Hình thoi là một trong những hình tứ giác thường gặp trong chương trình Toán tiểu học. Tuy nhiên, để tính được diện tích của hình thoi thì đòi hỏi các em học sinh lớp 5 phải nắm vững các kiến thức về hình thoi cũng như công thức tính chính xác. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về hình thoi, tính chất, dấu hiệu nhận biết và đặc biệt là các công thức tính diện tích hình thoi lớp 5 một cách chi tiết và dễ hiểu nhất.
Hình Thoi Là Gì?
Định Nghĩa
Hình thoi là một tứ giác có bốn cạnh bằng nhau.
Đặc Điểm
- Bốn góc đối diện bằng nhau.
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Hai đường chéo là đường phân giác của các góc đối diện.
Tính Chất Của Hình Thoi
Đặc Điểm Của Hình Thoi Là Tứ Giác
- Đối với bất kỳ hình thoi nào, ta luôn có tổng bốn góc bằng 360 độ, mỗi góc có số đo bằng 90 độ.
- Tổng bốn cạnh của hình thoi cũng bằng nhau.
- Hai đường chéo của hình thoi vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Hai đường chéo là đường phân giác của các góc đối diện.
Đặc Điểm Của Hình Thoi Là Hình Bình Hành
- Hình thoi có đầy đủ các tính chất của hình bình hành.
- Diện tích của hình thoi bằng diện tích của hình bình hành có cùng đáy và chiều cao.
- Hai đường chéo của hình thoi vuông góc với nhau.
Dấu Hiệu Nhận Biết Hình Thoi
Dấu Hiệu Nhận Biết Theo Đặc Điểm Của Tứ Giác
- Tứ giác có bốn cạnh bằng nhau.
- Tứ giác có hai đường chéo vuông góc với nhau.
Dấu Hiệu Nhận Biết Theo Đặc Điểm Của Hình Bình Hành
- Hình bình hành có hai cạnh kề bằng nhau.
- Hình bình hành có hai đường chéo vuông góc với nhau.
Cách Tính Diện Tích Hình Thoi Lớp 5
Công Thức Tính Dựa Vào Đường Chéo
Công thức:
Công Thức Dựa Vào Cạnh Đáy Và Chiều Cao
Công thức:
Lưu ý:
- Cạnh đáy là độ dài một cạnh bất kỳ của hình thoi.
- Chiều cao là độ dài đường vuông góc kẻ từ một đỉnh đến cạnh đối diện.
Công Thức Nếu Biết Một Góc Của Hình Thoi
Công thức:
Lưu ý:
- a là độ dài một cạnh bất kỳ của hình thoi.
- A là một góc bất kỳ của hình thoi.
Bài Tập Áp Dụng Công Thức Tính Diện Tích Hình Thoi Lớp 5
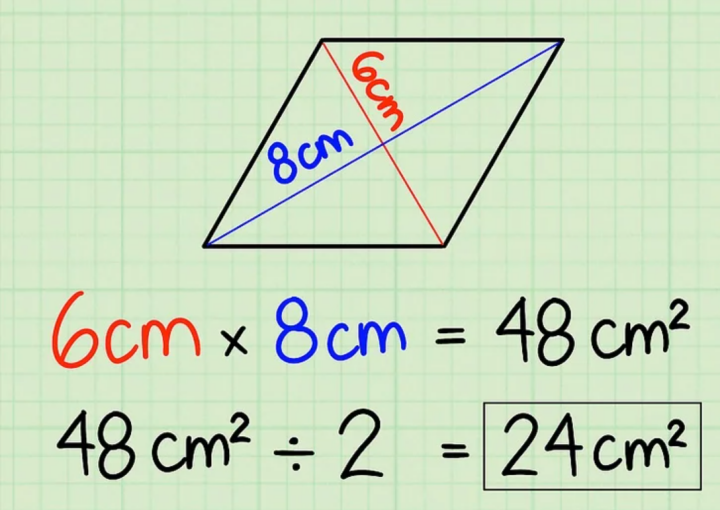
Bài 1:
Một hình thoi có độ dài hai đường chéo là 6cm và 8cm. Tính diện tích hình thoi đó.
Bài giải:
Diện tích hình thoi = $\frac$
Trên đây, chúng ta đã cùng nhau tìm hiểu về khái niệm hình thoi, tính chất, dấu hiệu nhận biết và các công thức tính diện tích hình thoi lớp 5 một cách chi tiết. Nắm vững những kiến thức này sẽ giúp các em học sinh giải quyết các bài toán liên quan đến hình thoi một cách dễ dàng và chính xác.
Hình thoi là một trong những hình tứ giác thường gặp trong chương trình Toán tiểu học. Tuy nhiên, để tính được diện tích của hình thoi thì đòi hỏi các em học sinh lớp 5 phải nắm vững các kiến thức về hình thoi cũng như công thức tính chính xác. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về hình thoi, tính chất, dấu hiệu nhận biết và đặc biệt là các công thức tính diện tích hình thoi lớp 5 một cách chi tiết và dễ hiểu nhất.
